In the catalogue we have two tables:
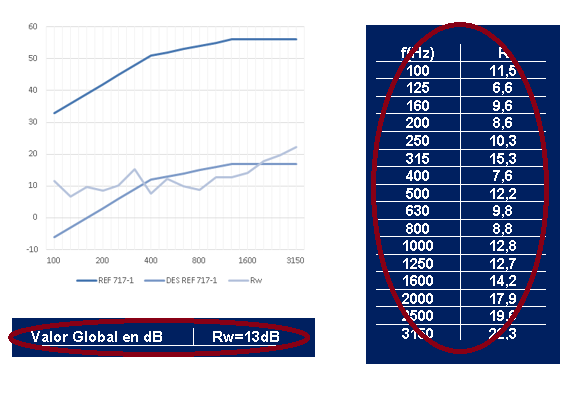
2-Global value of sound reduction index Rw | 1-Frequency values of the sound reduction index
1-Value of the acoustic reduction index by frequencies R:
What is frequency?
If we take a musical instrument, for example, a guitar, when one of its strings is plucked, it produces a sound – a musical note. To produce the musical note, the plucked string vibrates around its initial position. Frequency is measured in Hertz (Hz) and is defined as the number of times per second the string vibrates. Thus, when you tune your guitar, you are adjusting the tension of the string so that it vibrates at the desired frequency when is plucked. For example, the note A is tuned to 440Hz, so that each time that note is plucked, the string that generates it vibrates at a rate of 440 times per second.
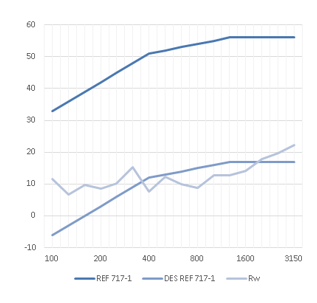
As sounds are made up of frequencies and the human ear does not perceive all frequencies in the same way, the UNE-EN ISO 10140-2 standard – and in general all standards related to acoustic insulation – establishes the frequencies at which the results should be presented, as these are considered to be the most representative. These frequencies are 100, 125, 160, 200, 250, 250, 315, 400, 500, 630, 800, 1000, 1250, 1600, 2000, 2500, 3150Hz. For each of these frequencies, the averaged value of the acoustic reduction index obtained from the averaging of the frequencies adjacent to them is given. At the 2500Hz frequency, for example, the tested acoustic curtain has a sound insulation index of 19,6dB. This means that for all sound waves with a frequency of 4000Hz, the acoustic curtain will reduce the sound pressure generated by them by 19,6dB.
2-Global Rw Value
This is the weight value in decibels obtained from the values of the sound reduction index for each one of the frequencies explained in the previous section.
What is a decibel (dB)?
The decibel is a unit of measurement widely used in telecommunications to express quantities of other units on a logarithmic scale. Thus, the word decibel can refer to several concepts. In the field of acoustics, decibels are used to measure both sound pressure and sound power.
To better understand what decibels are, let’s look at the following example:
Sound can be broadly defined as the physical phenomenon that occurs when an emitting body vibrates in a medium. When we speak, for example, our vocal cords vibrate, generating a sound wave.
As our vocal cords are in contact with the air – the medium – the wave generated creates pressure variations in the air, causing the particles that form it to vibrate. Thus, the air particles oscillate around their normal position, transmit the vibration to their neighbouring particles and then return to their initial position. In this way the sound wave propagates through the air particles at a speed that depends on the density and elasticity of the medium – approximately 340m/s in air.
When the wave reaches the receiver, it enters the ear and impacts with the eardrum. The impact of the wave is received as a nerve stimulus that the brain decodes as sound.
The discomfort these sound waves cause us is equivalent to the pressure they exert on the membrane of our ears and corresponds to what is colloquially known as the volume at which they are heard. The volume, therefore, can be equated with the pressure that the sound waves exert on the medium.
To normalise and measure sound pressure, sound level meters are used, the operation of which is inspired by that of the human ear. A sound level meter contains a microphone made up of a membrane that receives the pressure that sound waves exert on its surface when they impact on it. From a transducer, the value of the pressure exerted is obtained.
Sound pressure is measured in Pascals (P), after Pascal. However, in practice, the measurement in Pascals is converted to a logarithmic scale to normalise its value and is called sound pressure level, measured in decibels.
To normalise the decibel value, the following formula is used:
Lp = 20xlog (P / Pref)
Where Lp is the sound pressure level, i.e., the pressure value measured in decibels.
P is the pressure that the sound wave makes.
Pref is the reference value by which the measured sound pressure is normalised. It has a constant value of 2×10-5P.
Looking at the expression we see that it contains units of pressure in both the numerator and the denominator, the result being dimensionless. Therefore, the result is only expressed in dB (decibels) and not in decibels of Pascals (dBP). In other fields of telecommunications, units of measurement such as dBW are used, as they are not obtained from dimensionless expressions.
The reason for this standardisation is simple: since the decibel is only a unit of measurement that depends on another unit (in this case sound pressure), it was possible to establish a value to be used as a reference.
This is better understood if we look at it mathematically: if we take a sound wave that exerts a pressure on the membrane of our ears -or on the membrane of a loudspeaker- of 2×10-5P, applying the formula and the properties of logarithms, we will obtain the value of 0 decibels.
Thus, the value of 2×10-5P becomes the reference value in the new decibel scale. If we take any lower value, the result will be negative. And if we do the same with any higher value, the results will be positive.
The value of 2×10-5P is used as a reference because it corresponds to the threshold of human hearing. In other words, sounds that exert pressures on the membranes of our ears below this value are not perceived by our ears – colloquially put: the lowest volume we can hear. Thus, when converted to decibels, the values obtained greater than 0 correspond to the pressures that are perceptible to the human ear. As mentioned above, sound level meters have been developed inspired by the human ear. Therefore, the electronic circuits of sound level meters do not register pressures lower than the reference pressure either, so that in practice the dB values will always be higher than 0dB and therefore any dB value will always be a value perceptible to the human ear.
The sound pressure level representing the pain threshold is approximately 135-140dB.
Why are dBs used?
dB is used for two main reasons. The first is that, as explained in detail in the previous section, it allows us to normalise the pressure values so that we only have values of pressures that we can perceive. In addition, the logarithmic scale makes its assimilation easier. For example: If we take the value of the minimum threshold – the aforementioned 2×10-5P, corresponding to 0dB – and place the maximum at around 140dB, whose pressure is around 200P, we will have a too large range of numbers of pressure in Pascals. That is, the range of pressure values in Pascals is vast, making it unintuitive. Another example: if we have a sound wave that has a pressure of 2×10-3P, it is intuitively more difficult to establish whether it is a large or small value than if we compare it to its value in dB, which is 60dB.
The second reason why dB is used is related to human perception. Our auditory system does not respond in a linear way to sound stimuli. When our ear hears a pure tone of a certain sound pressure, if this pressure is doubled, the subjective perception does not interpret that the loudness has doubled, but subjectively perceives an increase of a lesser degree. In this way, the perception of the ear is better related to the values of the logarithmic scale.
Finally, we have a graph:
This graph shows the values of the sound reduction index R for the frequencies 100, 125, 160, 200, 250, 250, 315, 400, 500, 630, 800, 1000, 1250, 1600, 2000, 2500 and 3150 Hz.